- 圖文作者
- 牟善豪
- 使用軟體
- AutoCAD
在覘標中心不垂直於標石中心的情形下,先定出視準點於地面的投影位置,透過正弦定理間接得出偏心角後,再歸算至所求角度的計算方法。
觀測
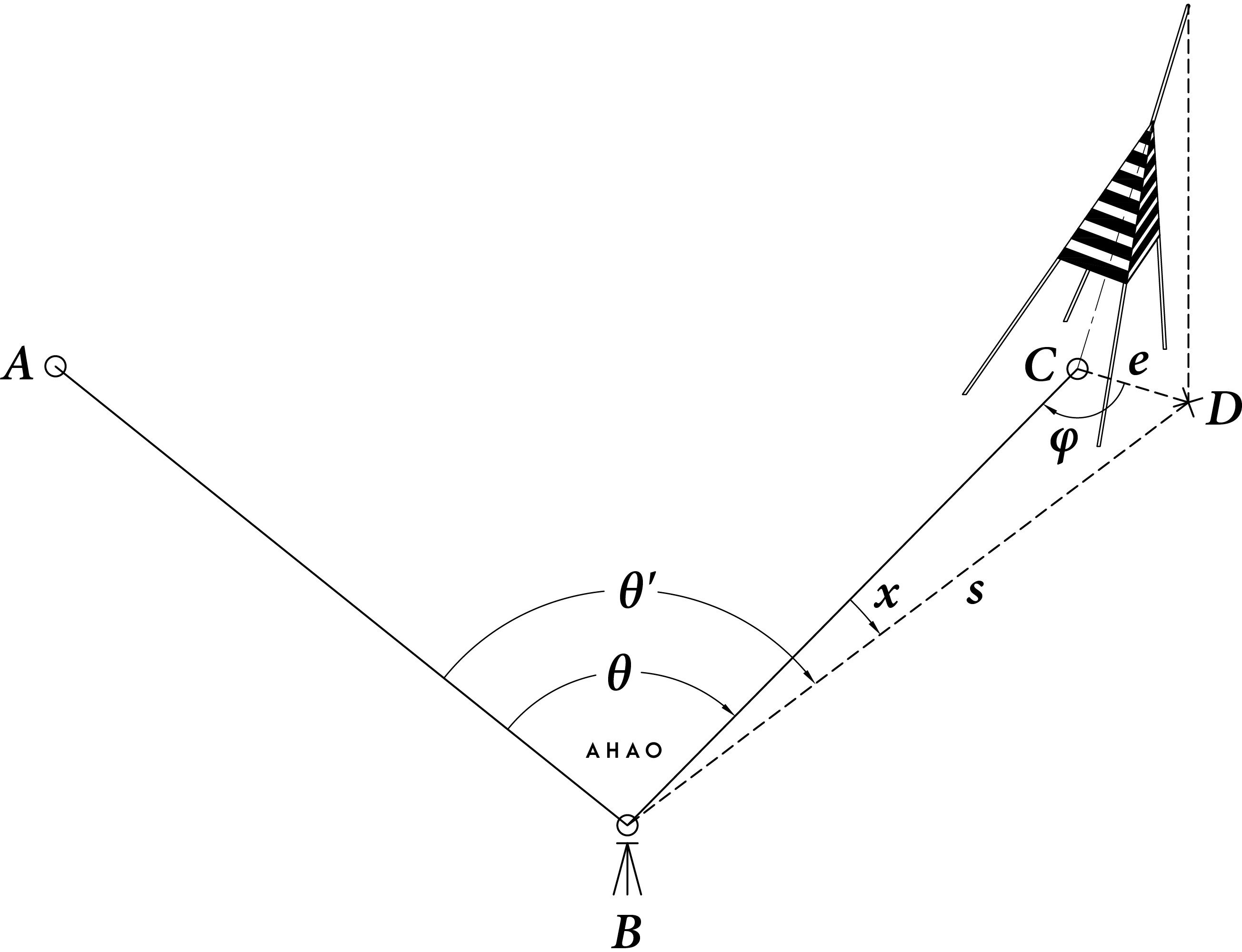
架設在野外的覘標,有時因受到自然環境或人爲外力等影響而傾斜,導致覘標中心與標石中心 $C$ 未能保持在同一垂直線上,發生視準點偏心。在此情形下,可利用十字交叉法,測定視準點在地面的投影位置 $D$,再量取 $C$、$D$ 兩點間的距離,以得出偏心距 $e$。
所謂十字交叉法,是將經緯儀設置在覘標附近,照準覘標視準點後,將望遠鏡垂直向下擺動,在地面上定出一直線段;再將經緯儀移至與該線段垂直方向的適當位置,以同樣方式定出另一直線段;此二線段的十字交叉點,卽爲視準點在地面的投影位置 $D$。
定出視準點在地面的投影位置 $D$ 之後,將經緯儀整置於測站 $B$,觀測 $\angle ABD$,卽 $\theta \ ^{\prime}$ 之值。透過正弦定理,可得出偏心角 $x$。以 $\theta \ ^{\prime}$ 減去 $x$,便能計算出所求角度 $\angle ABC$ 之值 $\theta$。
 計算
計算
偏心角 $x$:
\begin{gather*}
\frac {\sin x}{e}=\frac{\sin \varphi}{s}\\\\
\Rightarrow \ x=\sin^{-1} \left(\frac{e}{s} \cdot \sin \varphi \right)
\end{gather*}
角 $\theta$:
\begin{gather*}
\theta=\theta^{\ \prime}-x
\end{gather*}
判斷
當 $\varphi$ 大於 $180^{\circ}$ 時,$D$ 點必落在 $\angle ABC$ 的內側,$x$ 因而爲負值。
例題一(角 $\varphi$ 小於 $180^{\circ}$)
設視準點偏心距 $e=0.523 \ m$,將儀器設於 $C$ 站時,測得角 $\varphi= 70^\circ 55^\prime 13^{\prime\prime}$,再將儀器移至 $B$ 站,測得角 $\theta \ ^{\prime}= 83^\circ 33^\prime 26^{\prime\prime}$,已知 $s=1053.740 \ m$,試求角 $\theta$ 之值。
偏心角 $x$:
\begin{align}
x&=\sin^{-1} \left(\frac{e}{s} \cdot \sin \varphi \right)\\\\
&=\sin^{-1} \left(\frac{0.523}{1053.740} \cdot \sin \ 70^\circ 55^\prime 13^{\prime\prime} \right)\\\\
&=\ 0^\circ 01^\prime 36.75^{\prime\prime}
\end{align}
角 $\theta$:
\begin{align}
\theta&=\theta^{\ \prime}-x\\\\
&= \ 83^\circ 33^\prime 26^{\prime\prime}- \ 0^\circ 01^\prime 36.75^{\prime\prime}\\\\
&= \ 83^\circ 31^\prime 49.25^{\prime\prime}
\end{align}
例題二(角 $\varphi$ 大於 $180^{\circ}$)
設視準點偏心距 $e=0.617 \ m$,將儀器設於 $C$ 站時,測得角 $\varphi= 236^\circ 47^\prime 52^{\prime\prime}$,再將儀器移至 $B$ 站,測得角 $\theta \ ^{\prime}= 107^\circ 26^\prime 38^{\prime\prime}$,已知 $s=1176.230 \ m$,試求角 $\theta$ 之值。
偏心角 $x$:
\begin{align}
x&=\sin^{-1} \left(\frac{e}{s} \cdot \sin \varphi \right)\\\\
&=\sin^{-1} \left(\frac{0.617}{1176.230} \cdot \sin \ 236^\circ 47^\prime 52^{\prime\prime} \right)\\\\
&=-0^\circ 01^\prime 30.53^{\prime\prime}
\end{align}
角 $\theta$:
\begin{align}
\theta&=\theta^{\ \prime}-x\\\\
&= \ 107^\circ 26^\prime 38^{\prime\prime}-(-0^\circ 01^\prime 30.53^{\prime\prime})\\\\
&= \ 107^\circ 28^\prime 08.53^{\prime\prime}
\end{align}

0